MTU Department of Mathematics
Mathematics
Research Topics
- Complexity theory
- Geometric group theory
- Quantum groups
Publications & Talks
- J.P. McCarthy, Analysis for idempotent states on quantum permutation groups, Math Phys Anal Geom 28, 14 (2025). https://doi.org/10.1007/s11040-025-09511-5
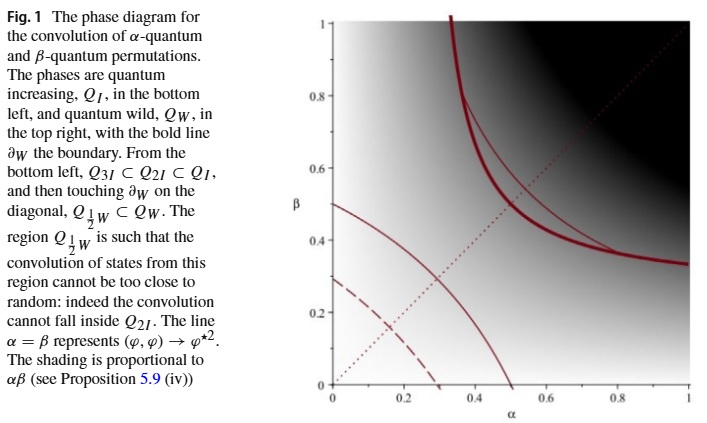
- J.P. McCarthy, Tracing the orbitals of the quantum permutation group, Arch. Math. 121, 211–224 (2023). https://doi.org/10.1007/s00013-023-01883-w
Abstract. Using a suitably noncommutative flat matrix model, it is shown that the quantum permutation group has free orbitals: that is, a monomial in the generators of the algebra of functions can be zero for trivial reasons only. It is shown that any strictly intermediate quantum subgroup between the classical and quantum permutation groups must have free three-orbitals. This is used to give explicit formulae for the Haar state on degree four monomials that hold for such intermediate quantum subgroups as well as the quantum permutation group itself.
- J.P. McCarthy, A quantum Frucht theorem, same talk given to Non local games seminar and C*-Days in Prague in May 2023.
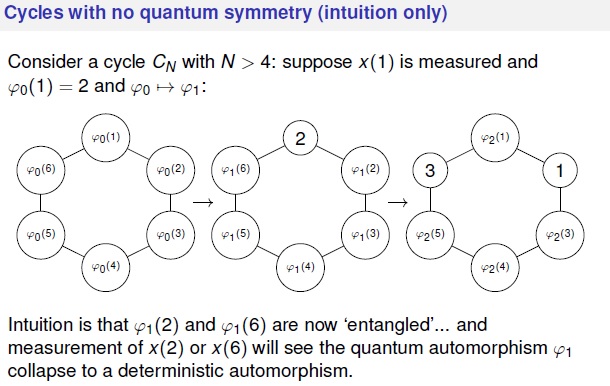
- J.P. McCarthy, Another look at idempotent states (on quantum permutation groups), talk given to Quantum Groups and Interactions workshop in Glasgow, May 2023.

- J.P. McCarthy, The Kawada-Ito theorem for quantum groups, UCC BRCI mini-Symposium on Noncommutative Probability & Quantum Information, October 2022.

- Shane O'Rourke, Affine structures, wreath products and free affine actions on linear non-archimedean trees, Journal of Lie Theory. 32 (2022), no. 1, 157-174.

- J.P. McCarthy, The Frucht property in the quantum group setting, Quantum Group Seminar, January 2022.

- J.P. McCarthy, A state-space approach to quantum permutations, Expositiones Mathematicae, 2021, ISSN 0723-0869, https://doi.org/10.1016/j.exmath.2021.12.003.

- Teo Banica and J.P. McCarthy, The Frucht property in the quantum group setting, Glasgow Mathematical Journal, 1-31, doi:10.1017/S0017089521000380
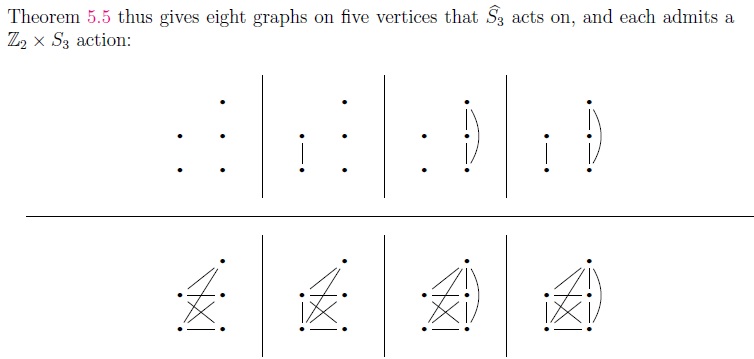
- J.P. McCarthy, The ergodic theorem for random walks on finite quantum groups, Communications in Algebra, DOI: 10.1080/00927872.2021.1908551

- J.P. McCarthy, Quantum Permuations Re-Born, Quantum Group Seminar (of Teo Banica, Universite de Cergy-Pontoise, Paris)

- J.P. McCarthy, The Ergodic Theorem for Random Walks: from Finite Groups, to Group Algebras, to Finite Quantum Groups, Munster Groups 2019, WIT.

- Shane O'Rourke, Free actions on metric lines. Talk at Groups and their Actions 2019 conference, Politecnica Slaska, Gliwice, Poland.
- J.P. McCarthy, Some Unresolved and Unexplored Aspects of Random Walks on Quantum Groups, Séminaire d’Analyse Fonctionnelle, Laboratoire de Mathématiques de Besançon, Université de Franche-Comté

- J.P. McCarthy, Diaconis--Shahshahani Upper Bound Lemma for Finite Quantum Groups, Fourier Anal Appl, 25, 2463--2491, 2019.
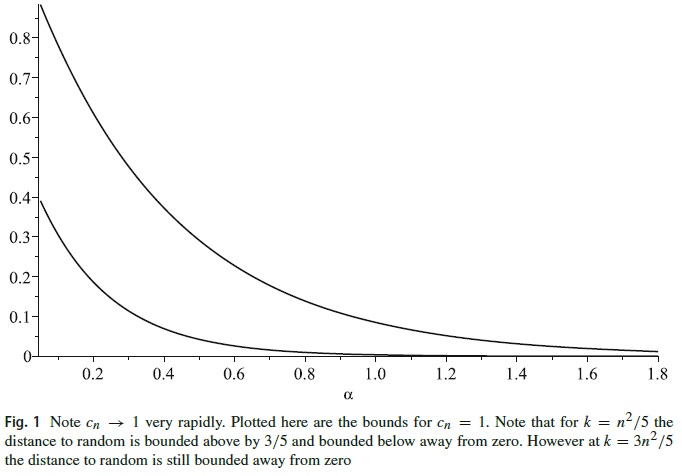
- J.P. McCarthy, The Diaconis-Shahshahani Upper Bound Lemma for Finite Quantum Groups, Irish Mathematical Society Meeting 2018, University College Dublin

-
Marie Nicholson, The complexity of Tukey types and cofinal types, CiE (Computability in Europe)
- J.P. McCarthy, The Diaconis-Shahshahani Upper Bound Lemma for Finite Quantum Groups, Topological Quantum Groups an Harmonic Analysis Workshop, Seoul National University.

-
Shane O'Rourke, A combination theorem for affine tree-free groups Int. J. Alg. and Comput. 26 (2016), 1283-1321.

- Shane O'Rourke, A combination theorem for affine tree-free groups. Talk at Geometric and Asymptotic Group Theory with Applications (GAGTA10) conference (Stevens Institute of Technology, New Jersey).
- J.P. McCarthy, CIT Department of Mathematics Spring Seminar Series, The Philosophy of Quantum Groups, January 2016.

- Shane O'Rourke, A combination theorem for affine tree-free groups. Invited speaker at Groups in Galway annual conference (NUI Galway).
- Shane O'Rourke, A tree-free group that is not orderable Proc. Amer. Math. Soc. 143 (2015), 41-43.


