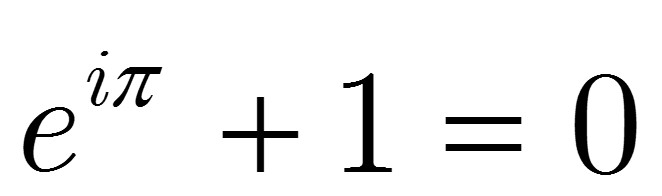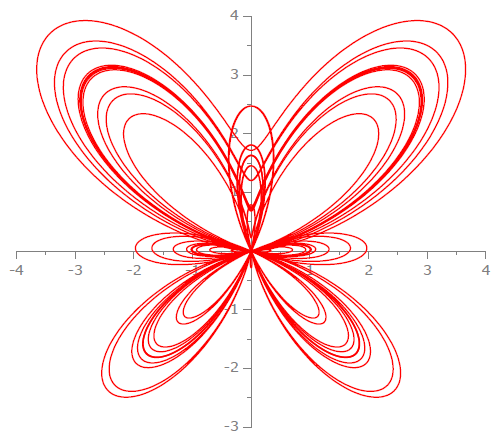The butterfly curve is a plane curve discovered by Temple H. Fay. The curve is given by the following parametric equations: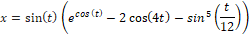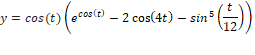

where .

There is beauty in numbers!

and so on.

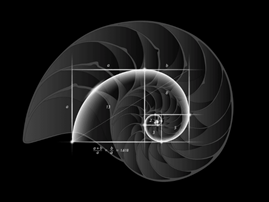
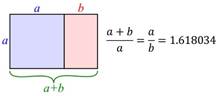
The Fibonacci sequence is the series of numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 and on to infinity. Each number is the sum of the previous two. Visualised, this sequence makes a spiral. Fibonacci numbers appear in nature often enough to prove that they reflect some naturally occurring patterns. Examples include shells, flower petals, seed heads, pinecones, galaxies, animal bodies, and many more.

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The figure below shows rectangles in golden ratio.

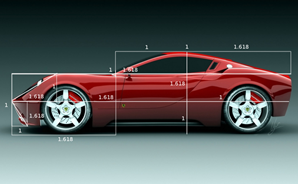
The golden ratio 1.618034 is commonly found in nature, and when used in design, it fosters organic and natural looking compositions that are aesthetically pleasing to the eye. Achieving beauty through harmony and proportion has been recognized for centuries in architecture, art and design.

If you take any two successive Fibonacci numbers, their ratio is very close to the golden ratio. As the numbers get higher, the ratio becomes even closer!

Fractals are some of the most beautiful and most bizarre geometric shapes. They look the same at various different scales – you can take a small extract of the shape and it looks the same as the entire shape. This curious property is called self-similarity.

Fractals are very popular in mathematical visualisation, because they look very beautiful. You can zoom into a fractal, and the patterns and shapes will continue repeating, forever. Figures (a) and (b) show some stunning computer generated fractals. There are of course equations and formulae involved behind these.Fractals are useful in modelling structures in which similar patterns recur at progressively smaller scales, for example snowflakes, crystal growth, and galaxy formation. They are also indispensable in computer-generated imagery used in movies and video games.

Fractals are also found in the geometry of the world around us (trees, mountains, lightning). Many natural fractals look as if they don’t have any order to them. However, if you examine them thoroughly, you would notice that they do have hidden logic to them. While there is no exact perfect symmetry in a tree, there’s usually ordered hierarchical repetition. The same shape keeps reappearing but changes the scale. Click here to watch a video simulation of a growing tree. Also see how in the Romanesco broccoli (image (c)) each tiny little spiral is an imitation of the floret as a whole.

More on fractals here and here.

(a)

(b)

(c)

"Euler's identity is amazing because it is simple to look at and yet incredibly profound. It comprises the five most important mathematical constants - zero (additive identity), one (multiplicative identity), e and pi (the two most common transcendental numbers) and i (fundamental imaginary number).

"Given that e, pi and i are incredibly complicated and seemingly unrelated numbers, it is amazing that they are linked by this concise formula”.

Prof David Percy, Institute of Mathematics and its Applications
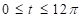